2023年学习记录 - 二叉树的性质和储存结构

声明

本节内容来源于 BiliBili视频数据结构与算法基础（青岛大学-王卓） 的 P81 - P85，本博客仅作笔记整理和学习记录，部分图片来自视频截图。

二叉树的性质

1. 在二叉树的第 $i$ 层上至多有 $2^{i-1}$ 个结点 $(i \geq 1)$。（证明：归纳法）
2. 深度为 $k$ 的二叉树至多有 $2^k-1$ 个结点 $(k \geq 1)$。（证明：性质1求和）
3. 对任何一棵二叉树 $T$，如果其叶子数为 $n_0$ ，度为 $2$ 的结点数为 $n_2$ ，则 $n_0=n_2+1$。（证明：边数证明）
4. 具有 $n$ 个结点的完全二叉树的深度为

   $$\lfloor log_2(n) \rfloor + 1$$

   （证明：n与k的关系）
5. 如果对一棵有 $n$ 个结点的完全二叉树的结点按层编号（从第 $1$ 层到第最后一层，每层从左到右），则对任一结点 $i(1 \leq i \leq n)$ ：
   • 如果 $i=1$，则结点 $i$ 是二叉树的根，无双亲；如果 $i > 1 $ ，则其双亲是结点：

   $$\lfloor i / 2 \rfloor$$

   • 如果 $2i>n$，则结点 $i$ 为叶子节点，无左孩子；否则其左孩子是结点 $2i$。
   • 如果 $2i+1>n$，则结点 $i$ 无右孩子；否则，其右孩子是结点 $2i+1$。
     （证明思路：归纳法）

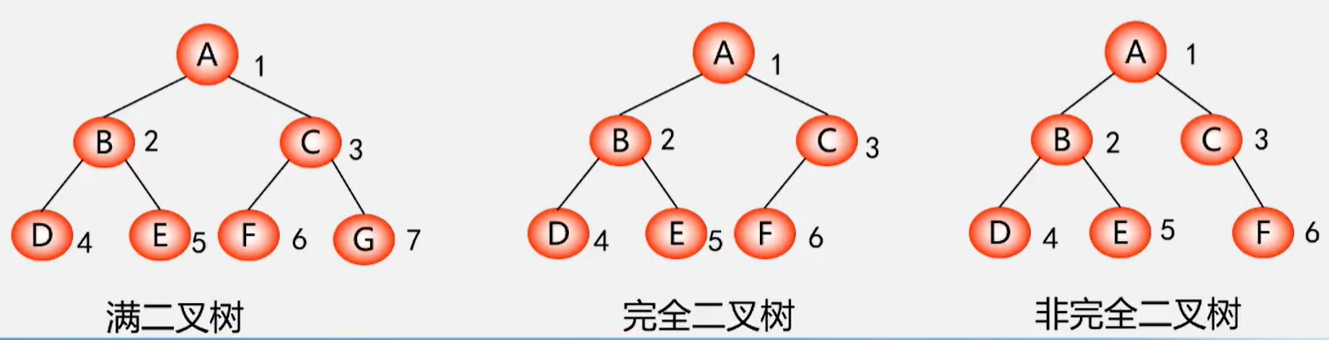
满二叉树

定义：一颗深度为 $k$ 且有 $2^k-1$ 个结点的二叉树称为满二叉树。

特点：

1. 每一层上的结点数都是最大结点数（即每层都满）。
2. 叶子结点全部在最底层。
3. 满二叉树在同样深度的二叉树中结点、叶子节点个数最多。

编号规则：自上而下，自左而右。

完全二叉树

深度为 $k$ 的具有 $n$ 个结点的二叉树，当且仅当其中每一个结点都与深度为 $k$ 的满二叉树中编号为 $1~n$ 的结点一一对应时，称之为完全二叉树。

在满二叉树中，从最后一个结点开始，连续去掉任意个结点，即是一颗完全二叉树。

特点：

1. 叶子只可能扽不在层次最大的两层上。
2. 对任一结点。如果其右子树的最大层次为 $i$，则其左子树的最大层次必为 $i$ 或 $i+1$。

二叉树的存储结构

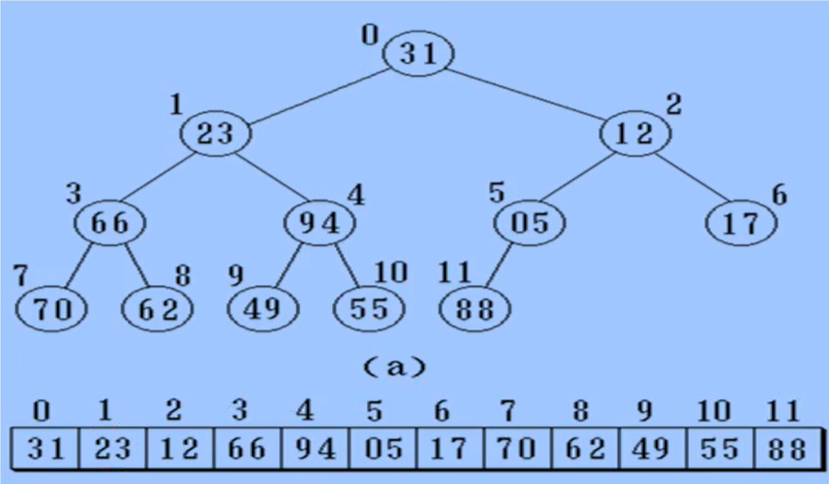
二叉树的顺序存储存储

实现：按满二叉树的结点层次编号，依次存放二叉树中的数据元素。

// 二叉树顺序存储表示
#define MAXTSIZE 100
Typedef TElemType SqBiTree[MAXTSIZE]
SqBiTree bt;

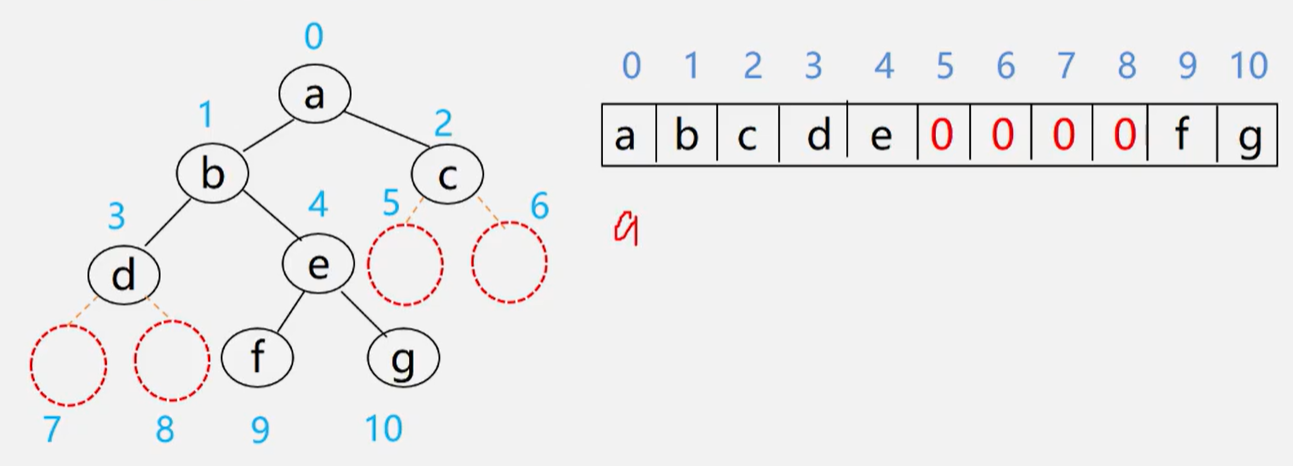
二叉树的顺序存储缺点：
最坏情况：深度为 $k$ 的且只有 $k$ 个结点的单支树需要长度为 $2^k-1$ 的一维数组。

特点：

• 结点间关系蕴含在其存储位置中。
• 浪费空间，适于存满二叉树和完全二叉树。

二叉树的链式存储

// 二叉树的链式存储定义
typedef struct BiNode{
  TElemType data;
  struct BiNode *lchild, *rchild;
}BiNode, *BiTree;

在 $n$ 个结点的二叉链表中，必有 $2n$ 个链域，会有 $n-1$ 个结点的链域存放指针，会有 $n+1$ 个空指针域。

Tip：空指针域可以在线索二叉树中被利用。

三叉链表

// 三叉链表定义
typedef struct TriTNode{
  TElemType data;
  struct TriTNode *lchild, *parent, *rchild;
}TriTNode, *TriTree;